湘江电力电缆主要电气参数计算以及计算实例

返回列表来源：湘江电缆发布日期 2016-10-19 02:47浏览：- 加入收藏

湘江电缆为您导读：电力电缆在电力工程设计和施工过程中，如何计算该电力电缆的直流电阻，交流电阻、电感、阻抗、电压降及电容，是电力设计师和负责施工的工程师必须要掌握的。下面是小编整理的电力电缆主要电气参数计算，小编还细心的列举的一个计算实例，是不是特别有爱？

那么，现在就正式开始咱们今天的学习！

1.设计电压

电力电缆及附件的设计必须满足额定电压、雷电冲击电压、操作冲击电压和系统最高电压的要求。其定义如下：

额定电压

额定电压是电缆及附件设计和电性试验用的基准电压，用U0/U表示。

U0——电缆及附件设计的导体和绝缘屏蔽之间的额定工频电压有效值，单位为kV；

U——电缆及附件设计的各相导体间的额定工频电

压有效值，单位为kV。

雷电冲击电压

UP——电缆及附件设计所需承受的雷电冲击电压的峰值，既基本绝缘水平BIL，单位为kV。

操作冲击电压

US——电缆及附件设计所需承受的操作冲击电压的峰值，单位为kV。

系统最高电压

Um——是在正常运行条件下任何时候和电网上任何点最高相间电压的有效值。它不包括由于故障条件和大负荷的突然切断而造成的电压暂时的变化，单位为kV。

定额电压参数见下表

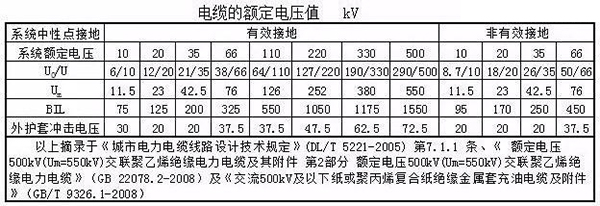
330kV操作冲击电压的峰值为950kV；500kV操作冲击电压的峰值为1175kV。

2.导体电阻

2.1导体直流电阻

单位长度电力电缆的导直流电阻用下式计算:

式中：

R＇——单位长度电缆导体在θ℃温度下的直流电阻；

A——导体截面积，如导体右n根相同直径d的导线扭合而成，A=nπd2/4;

ρ20——导体在温度为20℃时的电阻率，对于标准软铜ρ20=0.017241Ω˙mm2/m：对于标准硬铝：ρ20=0.02864Ω˙mm2/m；

α——导体电阻的温度系数（1/℃）；对于标准软铜：=0.00393℃-1；对于标准硬铝：=0.00403℃-1；

k1——单根导线加工过程引起金属电阻率的增加所引入的系数。一般为1.02-1.07（线径越小，系数越大）；具体可见《电线电缆手册》表3-2-2；

k2——用多根导线绞合而成的线芯，使单根导线长度增加所引入的系数。对于实心线芯，=1；对于固定敷设电缆紧压多根导线绞合线芯结构，=1.02（200mm2以下）～1.03（240mm2以上）

k3——紧压线芯因紧压过程使导线发硬、电阻率增加所引入的系数（约1.01）；

k4——因成缆绞合增长线芯长度所引入系数，对于多芯电缆及单芯分割导线结构，（约1.01）；]

k5——因考虑导线允许公差所引入系数，对于紧压结构，约1.01；对于非紧压型，k5=[d/(d-e)]2（d为导体直径，e为公差）。

20℃导体直流电阻详见下表：

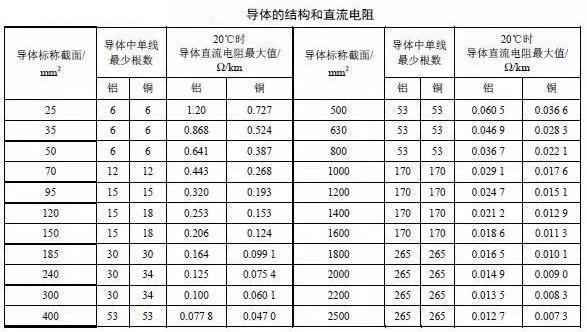
以上摘录于《10(6)kV～500kV电缆技术标准》（Q∕GDW371-2009）。

2.2导体的交流电阻

在交流电压下，线芯电阻将由于集肤效应、邻近效应而增大，这种情况下的电阻称为有效电阻或交流电阻。

电力电缆线芯的有效电阻，国内一般均采用IEC-287推荐的公式:

R=R′(1+YS+YP)

式中：

R——最高工作温度下交流有效电阻，Ω/m；

R′——最高工作温度下直流电阻，Ω/m；

YS——集肤效应系数，YS=XS4/(192+0.8XS4)，

XS4=（8πf/R′×10-7kS）2；

YP——邻近效应系数，YP=XP4/(192+0.8XP4)(Dc/S)2{0.312(Dc/S)2+1.18/[XP4/(192+0.8XP4)+0.27]}，XP4=（8πf/R′×10-7kP）2。

XS4——集肤效应中频率与导体结构影响作用；

XP4——邻近效应中导体相互间产生的交变磁场影响作用；

f——频率；

Dc——线芯直径，m；

S——线芯中心轴间距离，m；

ks——线芯结构常数，分割导体ks=0.435，其他导体ks=1.0；

kp——线芯结构系数，分割导体kp=0.37，其他导体kp=

0.8~1.0；

对于使用磁性材料制做的铠装或护套电缆，Yp和Ys应比计算值大70%，即:

R=R′[1+1.17(YS+YP)]

3.电缆的电感

3.1自感

则单位长度线芯自感：

Li=2W/(I2L)=μ0/(8π)=0.5×10-7

式中：

Li——单位长度自感，H/m；

μ0——真空磁导率，μ0=4π×10-7，H/m；

以上一般是实心圆导体，多根单线规则扭绞导体如下表：

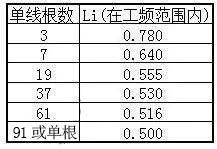
因误差不大，计算一般取Li=0.5×10-7H/m。

3.2高压及单芯敷设电缆电感

对于高压电力电缆，一般为单芯电缆，若敷设在同一平面内（A、B、C三相从左至右排列，B相居中，线芯中心距为S），三相电路所形成的电感根据电磁理论计算如下：

对于中间B相：

LB=Li+2ln(2S/Dc)×10-7(H/m)

对于A相：

LA=Li+2ln(2S/Dc)×10-7-α(2ln2)×10-7(H/m)

对于C相：

LC=Li+2ln(2S/Dc)×10-7-α2(2ln2)×10-7(H/m)

式中：

实际计算中，可近似按下式计算：

LA=LB=LC=Li+2ln(2S/Dc)×10-7(H/m)

同时，经过交叉换位后，可采用三段电缆电感的平均值，即：

L=Li+2ln(2×(S1S2S3)1/3/Dc)×10-7(H/m)

=Li+2ln(2×21/3S/Dc)×10-7(H/m)

对于多根电缆并列敷设，如果两电缆间距大于相间距离时，可以忽略两电力电缆相互影响。

3.3三相电缆的电感

主要计算中低压三相电缆三芯排列为“品”字形电缆。根据电磁场理论，三芯电缆工作电感为：

L=Li+2ln(2S/Dc)×10-7

式中：

L——单位长度电感，H/m；

S——电缆中心间的距离，m；

若三芯电缆电缆中心间的距离不等距，或单芯三根品字排列时三相回路电缆的电感按下式计算：

式中：

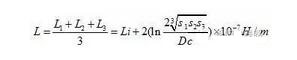
S1、S2、S3——电缆各相中心之间的距离，m。

4.电缆金属护套的电感

4.1三角排列

三根单芯电缆按等边三角形敷设的三相平衡负载交流回路，护套开路，每相单位长度电缆金属护套的电感为：

Ls=2ln(S/rs)×10-7(H/m)

式中：

rs——电缆金属护套的平均半径，m。

4.2等距直线排列

三根单芯电缆按等距离平面敷设的三相平衡负载交流回路，护套开路，每相单位长度电缆金属护套的电感为：

对于中间B相：

LSB=2ln(S/rs)×10-7(H/m)

对于A相：

LSA=2ln(S/rs)×10-7-α(2ln2)×10-7(H/m)

对于C相：

LSC=2ln(S/rs)×10-7-α2(2ln2)×10-7(H/m)

式中：

三相平均值：

LS=2ln(S/rs)×10-7+2/3?ln2×10-7(H/m)

4.3任意直线排列

三根单芯电缆平面敷设的三相平衡负载交流回路，电力电缆换位，护套开路，每相单位长度电缆技术护套的电感为：

LSB=2ln(((S1S2S3)1/3)1/3/rs)×10-7(H/m)

5.电缆电抗、阻抗及电压降

5.1电抗

电缆的电抗为：

X=ωL(Ω/m)

式中：

L——电缆单位长度的电感，H/m;

ω=2πf。

5.2阻抗

电缆的阻抗为：

Z=（R2+X2）1/2(Ω/m)

式中：

R——电缆单位长度的交流有效电阻，Ω/m。

5.3电压降

电缆的电压降为：

△U=IZl(V)

式中：

I——导体电流，A；

l——电缆长度，m。

6.电缆的电感

电缆的电容是电缆中的一个重要参数，它决定电缆线路的输送容量。在超高压电缆线路中，电容电流可能达到电缆额定电流的数值，因此高压电缆必须采取措施（一般采取交叉互联）抵消电容电流来提高缆线路的输送容量。

电缆电荷量与电压的的比值则为该电缆的电容。

相电压：

u=q/(2πε0ε).ln(Di/Dc)

所以电缆单位长度的电容为：

C=q/u=2πε0ε/ln(Di/Dc)

式中：

Di——绝缘外径，m；

ε——绝缘介质相对介电常数，交联聚乙烯ε=2.5，聚乙烯ε=2.3，聚氯乙烯ε=8.0，F/m；

ε0——真空绝对介电常数，ε0=8.86×10-12，F/m；

7.计算实例

一条电力电缆型号YJLW02-64/110-1X630长度为2300m,导体外径Dc=30mm，绝缘外径Di=65mm，电缆金属护套的平均半径rs=43.85，线芯在20°C时导体电阻率ρ20=0.017241×10-6Ω˙m，线芯电阻温度系数α=0.00393℃-1，k1k2k3k4k5≈1，电缆间距100mm，真空介电常数ε0=8.86×10-12F/m，绝缘介质相对介电常数ε=2.5,正常运行时载流量420A。计算该电缆的直流电阻，交流电阻、电感、阻抗、电压降及电容。

计算如下：

1.直流电阻

根据直流电阻公式：

得：

R＇=0.017241×10-6(1+0.00393(90-20))/(630×10-6)

=0.3489×10-4（Ω/m）

该电缆总电阻为R=0.3489×10-4×2300=0.08025（Ω）

2.交流电阻

由公式YS=XS4/(192+0.8XS4)，XS4=（8πf/R′×10-7kS）2得：

XS4=(8×3.14×50/0.3489×10-4)×10-14=12.96

YS=12.96/(192+0.8×12.96)=0.064

由公式XP4=（8πf/R′×10-7kP）2得：

XP4=(8×3.14×50/0.3489×10-4)×10-14=12.96

由公式YP=XP4/(192+0.8XP4)(Dc/S)2{0.312(Dc/S)2+1.18/[XP4/(192+0.8XP4)+0.27]}得：

YP=12.96/(192+0.8×12.96)(30/100)｛(0.312(30/100)+1.18/(12.96/(192+0.8×12.96)+0.27)｝=0.02

有公式R=R′(1+YS+YP)得：

R=0.3489×10-4(1+0.064+0.02)=0.378×10-4(Ω/m)

该电缆交流电阻RZ=0.378×10-4×2300=0.8699(Ω)

3.电感

由公式L=Li+2ln(2S/Dc)×10-7得到单位长度电感：

L1=0.5×10-7+2ln(2×100/65)×10-7=2.75×10-7（H/m）

该电缆总电感为L=2.75×10-7×2300=0.632×10-3H

4.金属护套的电感

由公式LS=2ln(S/rs)×10-7+2/3?ln2×10-7得到单位长度金属护套的电感：

LS1=2ln(100/43.85)×10-7+2/3?ln2×10-7

=2.11×10-7H/m

该电缆金属护套的电感为LS=2.11×10-7H/m×2300=0.4855×10-3H

5.电抗、阻抗及电压降

由公式X=ωL得到电抗：

X=2πf×0.632×10-3=0.199Ω

由公式Z=（R2+X2）1/2得到阻抗：

Z=（0.86992+0.1992）1/2=0.8924Ω

由公式△U=IZl得到电压降为：

△U=500×0.8924Ω=374.8V

6.电容

由公式C=2πε0ε/ln(Di/Dc)得到单位长度电容：

C1=2×3.14×8.86×10-12×2.5/Ln(65/30)=0.179×10-6F/m

该电缆总电容为C=0.179×10-6×2300=0.411×10-3F